Parallel & Perpendicular Lines

Hey everyone .. guess what time it is?




It's peanut bu --- scriiiiibe time! :D

Haha, everyone loves the dancing banana. Well anyways, it's Jackie here. This is my first whack at scribing so don't mind me of I sound totally out of line .. don't say i didn't warn you. d: Oh, and thank you Wendy for your post prior to this. That was very sweet of you, big heart. (: Well, getting on to business, let's have a look at what we learned today in classroom 69.

:D

Today, Mrs. Ingram established the relevance of graphing parallel and perpendicular lines, and how to calculate them. The lesson started off with graphing our first line, given the equation -2x + y = 6. We want to find the slope intercept of this equation so that we can set it up on a graph.

SLOPE INTERCEPT FORM :y = mx + b
where m = slope.
where b = y-intercept.

So, once we rearrange this equation into slope-intercept form, we get y = 2x + 6. Here, I will demonstrate how to calculate your slope and y-intercept ..

- 2x + y = 6
+ 2x + 2x
--------------
y = 2x + 6
m = 2/1 ; b = 6

Because we've already singled out the y, we now know that our slope (m) = 2/1, and that our y-intercept (b) = 6. Now, you can see how we graph this on my girly pink graph template .. =D

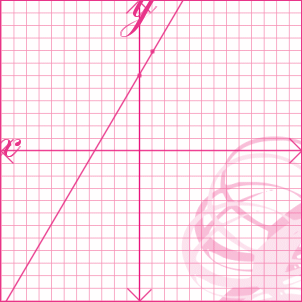
oh, just a friendly reminder .. always remember to label your x-axis and y-axis, as well as mark the arrows on your lines to indicate that they continue in both directions .. sorry, i was lazy to mark them on my graph but i think you get the point. :)

Now that we have our first line on the graph, we were given our second line to graph. The equation was -4x + 2y = -2. Following the same procedures as to what we did with the first equation, we rearrange the equation into slope-intercept form to find .. you guessed it, the slope and the y-intercept.

-4x + 2y = -2
+ 4x + 4x
--------------
2y = 4x - 2
___________
2
y = 2x - 1

m = 2/1 ; b = -1

Surprise, now it's time to put our second line on the graph.

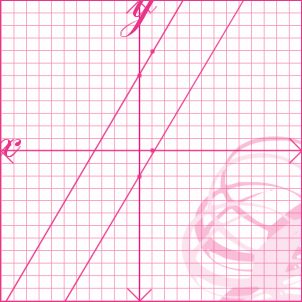
Now, looking at the graph .. you see that both the lines that we have traced onto the graph are parallel (//), meaning that they will continue both ways and never meet.

Wasn't that fun? (: Okay, now here's something new. We were given a third line to put onto the graph ..

x + 2y = 12
- x - x
-------------
2y = -x + 12
____________
2
y = -x/2 + 6
m = -1/2 ; b = 6

Now that we calculated our third line, we trace it onto the graph like so ..

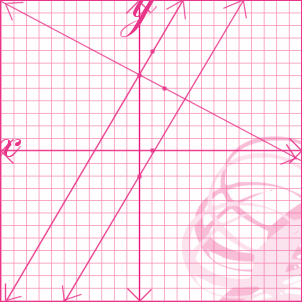
Looking at the graph, we can see that the first and third line that we made are perpendicular, meaning they cross each other. To determine the perpendicular line of a given slope, we calculate the negative reciprocal. This basically means that we turn it over and change the sign.

ex: m = -3/2
m (penpendicular, don't have the symbol for it on the keyboard :|) = -2/3

We were given a few sample questions to solve that helped us better understand this "perpendicular/parallel" line theory .. majig.

* question one: Write the equation of a line that passes through (-2,4) and is perpendicular to 2x - 3y + 5 = 0.
1: Calculate the slope of the existing line.
You do this by rearranging the equation into slope-intercept form. y = mx + b

2x - 3y + 5 = 0
+ 3y + 3y
--------------------
2x + 5 = 3y
___________
3
2x/3 + 5/3 = y
m = 2/3 ; b = 5/3

2: What's the perpendicular slope?
m = 3/2 .. so !
m (perpendicular) = -3/2

3: Determine the equation using the point-slope form. In the equation, replace all the terms that you arleady know and solve from then on.

y - y1 = m ( x - x1 )
(2) y - 4 = -3/2 ( x + 2 ) (2)
2 ( y - 4 ) = -3 ( x + 2 )
2y - 8 = -3x - 6
+ 8 + 8
----------------
2y = -3x + 2
___________
2
y = -3x/2 + 1

general form: 3x + 2y = 2
standard form: 2x + 2y - 2 = 0

* question two: Determine the equation of a line with the x-intercept of 2 and is parallel to the line 3x - 2y = 6.

1: Calculate the slope of the existing line.
You do this by rearranging the equation into slope-intercept form. y = mx + b

3x - 2y = 6
(Remember, when switching values from one side of the equation to the other, negatives become positives and vice-versa.)
3x - 6 = 2y
___________
2
3x/2 - 3 y
m = 3/2 ; b = -3

2: What's the perpendicular slope?
m = 3/2 .. so !
m (perpendicular) = -2/3

3: Determine the equation using the point-slope form. y - y1 = m ( x - x1 ) In the equation, replace all the terms that you arleady know and solve from then on.

y - y1 = m ( x - x1 )
(2) y - 0 = 3/2 ( x - 2 ) (2)
2y = 3 ( x - 2 )
2y = 3x - 6
___________
2
y = 3x/2 - 3

general form: 3x/2 - y = 3
standard form: 3x/2 - y - 3 = 0

Well, that's basically all you need to know on what we've learned today in class on parallel & perpendicular lines. We were assigned exercise 14, omitting questions 10 & 11. Well, that was pretty easy right? Good luck to everyone with the questions .. and trying to understand my scribe. d: that's all for now, folks. :)

And a do - doodle - loo - do .. ?

Scribe List

Wendy_V
natasha
Mary Ann
kaeser
jamielyn__
paulle
aneehs
[ jackie d. ]
sunly
Sean
Thoroughbred
im cool =P
031215
kimD
Marcus
mae'L
geliiker

i know its late...

Its never to late to say happy birthday right?... well i know its almost an hour that has past but ..... i have an announcement to make.

MARCH 4th
(YESTERDAY) 49 minutes ago)

.... WAS JACKIE.D's BIRTHDAY ....

sooo.. i would like to say to our special class mate Jackie D.

HAPPY BIRTHDAY JACKIE.
MAY ALL YOUR WISHES COME TRUE
AND MAY YOU ENJOY EVERY LITTLE SECOND ON THAT SPECIAL DAY.

-+-Scriber-+-

hey everyone, i'm today's scribe. we started off class with our linear equations (graphing each equation) handed back. then Mrs. Ingram started us off with 3 example of changing an equation into the slope-intercept form.
Slope-Intercept form = y = mx + b
( m = slope, b = intercept )

The three examples were :
Change to the Slope-Intercept Form

Example Number 1.
1. 21y = 15 - 27x
= 21y/21 = -27x/21 + 15/21
= 7y/7 = -9/7 + 5/7
= y = -9/7 + 5/7

Step 1. ---> Change the equation to the Slope-Intercept Form.
Step 2.---> The first point on the graph, will be the y-intercept. (0, 5/7)
Step 3. ---> Locate the second point using the Slope. ( -9/7 = rise/run )

You then, should have a graph looking like this one;















Example Number 2.
2. 7x + 2y = -22
= 2y = -7x - 22
= 2y/2 = -7x/2 - 22/2
= y = -7/2 x - 11

You then, should end up with a graph looking like this;
















Example Number 3.
3. x = 7y/5 + 21/5
( you find the commen denominator and multiply everything by the commen denominator which is 5)
= 5x = 7y + 21
= 5x/7 - 21/7 = 7y/7
= 5x/7 - 3 = y

You then should have a graph looking like this;















If you had no problem and had a good understanding of those 3 examples then you would be just fine on the worksheet that was handed to us today in class.

Tonight's homework is the Linear Equation (Write the slope-intercept form of the equation). Do questions 4, 6, 12, 15, 16. Graph is to be handed in the beginning of tomorrows class.

LALALALALALALALLALALALALALALALALALALALALALALALALALALALALALALALALALAL LALALALALALALALALALALALALALALALALALALALALALALALALALALALALALALALLALAL
*drums...... tomorrows scribe will be NATASHA .. :O... wow no one expected that! "hahahah" good luck! =p

Scribe Post

Today in class we looked at graphing straight line equations using the "slope-intercept" format.
To do this we must first change the equation into the format y = mx + b, where m( is the slope) and b ( is the y-intercept )
Once in this form the first point we place on the graph is the y-intercept. ( the b value)
Then remembering that slope is the rise/run, we start at the y-intercept and move up or down, then left or right using the slope value to locate the second point.
With 2 points from the line we can draw the line, ensuring that we place arrows at either end of the line.
Just like that the line is graphed.
Assignment was Exercise 12, questions 1 - 9, 11 - 15.
Also a graphing handout which is to be handed in at the beginning of Tuesday's class.

First Post

This is the beginning of the S2 Pre-Calculus blog.
Enjoy.